在当今社会,数学的重要性不言而喻,它不仅是我们认识世界、改造世界的理性工具,更是培养逻辑思维和解决问题能力的关键。然而,数学史作为数学发展的见证,同样具有不可忽视的价值。通过了解数学史,我们可以更深入地理解数学思想的演变,感受数学作为人类文化成就的独特魅力。
日本著名数学家矢野健太郎的著作《一口气读完的数学史:从手指计数到AI文明》以简洁明了的笔触,为读者勾勒出数学史的发展脉络。从史前时代人类对数的初步认识,到五进制、十进制等记数方法的形成,再到0的发现、方程的发展、对数的诞生,以及解析几何、微积分等重大突破,这本书用轻松的语言将复杂的数学史娓娓道来。
在书中,矢野健太郎特别提到了拓扑学这一数学分支的起源。拓扑学,这个看似抽象的概念,其发源地竟是一座历史悠久的城市——哥尼斯堡(现为加里宁格勒)。哥尼斯堡七桥问题,一个看似简单却难以解答的谜题,激发了数学家欧拉的兴趣。他巧妙地将七桥问题转化为一笔画问题,并据此提出了拓扑学的基本概念,即图形在形变过程中性质保持不变。
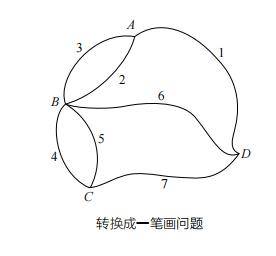
欧拉的一笔画定理指出,一个图形要能一笔画成,必须满足引出奇数条线的点为起点或终点。这一定理不仅解决了哥尼斯堡七桥问题,还为拓扑学的发展奠定了基础。通过拓扑变换,我们可以观察到图形在形变过程中保持不变的性质,这些性质构成了拓扑学研究的核心。
除了拓扑学,书中还介绍了多面体、简单闭曲线、单连通区域和多连通区域等概念。矢野健太郎通过生动的例子和直观的图形,让读者轻松理解这些抽象的概念。例如,他通过统计正多面体的顶点数、边数和面数,得出了欧拉定理:对于亏格为0的多面体,顶点数减边数再加面数的结果恒等于2。这一定理不仅在数学领域具有重要地位,还广泛应用于计算机科学、物理学等其他领域。
矢野健太郎的《一口气读完的数学史》自上市以来,已重印70多次,成为经久不衰的经典之作。它不仅让读者在轻松愉快的阅读中了解数学史的发展脉络,更激发了人们对数学的兴趣和热爱。通过这本书,我们可以感受到数学的魅力所在,它不仅是科学的语言,更是人类智慧的结晶。