在近日的教育领域中,高中数学的重点题型成为了热议话题。一系列精心挑选的题型,不仅涵盖了三角函数、数列,还深入探讨了导数和圆锥曲线的应用,为学生们提供了全面的复习指南。
三角函数题型以其灵活多变著称,要求学生熟练运用同三角函数关系、诱导公式以及和、差、倍、半等公式进行化简求值。例如,某些题目会考察学生如何通过公式转换,求解复杂三角函数表达式的值。
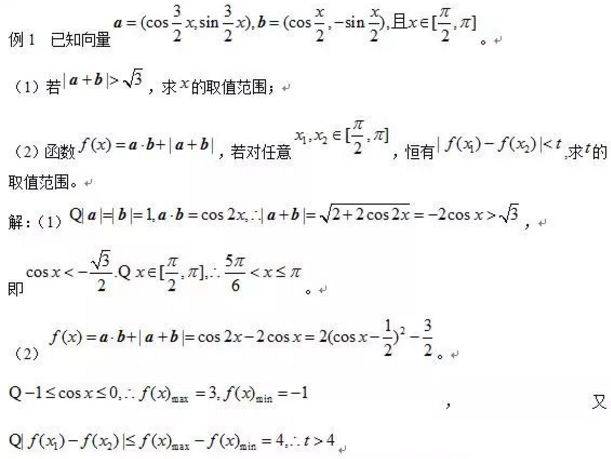
运用三角函数性质解题也是考试中的常见题型,这通常涉及正弦、余弦函数的单调性、周期性、最值、对称轴及对称中心的考察。学生们需要深入理解这些性质,才能准确解答相关题目。
数列题型则侧重于通项公式和前n项和的求法。这类题目不仅要求学生掌握等差数列、等比数列的基本公式,还常常结合递推数列、复合数列等复杂形式,考察学生的逻辑思维和解题技巧。


导数题型则更加注重函数的极值、最值以及单调性的研究。通过导数,学生们可以深入了解函数的性质,从而解决一系列实际问题。例如,利用导数研究函数的极值、最值,可以帮助学生们找到函数的最优解;而利用导数的几何意义求切线方程,则是解析几何中的重要应用。


最后,圆锥曲线题型以其几何直观性和代数复杂性相结合的特点,成为了高中数学中的难点和重点。这类题目通常要求学生通过数形结合的方法,确定直线和圆锥曲线的位置关系,进而求解相关问题。例如,焦点三角函数、焦半径、焦点弦等问题,都需要学生们具备扎实的几何基础和代数技巧。