在中小学生的教育世界里,阅读被视为激发学生兴趣的重要源泉。著名教育家苏霍姆林斯基曾坚定地说:“我深信书籍拥有巨大的教育力量。”这句话在教育界广为流传,成为许多教师心中的座右铭。
近日,我们特别关注了六年级上册数学中的《分数乘法》这一章节,它不仅是数学学习中的重要一环,也是培养学生逻辑思维和问题解决能力的关键。

分数乘法的意义分为两部分:一是分数乘整数,这与整数乘法的意义相同,即求几个相同加数的和的简便运算;二是一个数(无论是小数、分数还是整数)乘分数,这表示该数的几分之几是多少。在计算法则上,整数与分数相乘时,整数与分子相乘的积作为新的分子,分母保持不变;而分数与分数相乘时,则是分子相乘的积作为新的分子,分母相乘的积作为新的分母。
分数大小的比较也是分数乘法中的一个重要知识点。当一个数(0除外)乘以一个真分数时,结果小于原数;乘以一个假分数时,结果等于或大于原数;乘以一个带分数时,结果大于原数。这些规律在解决实际问题时非常有用。
在解决实际问题时,分数应用题通常遵循一定的解题步骤。首先要找出含有分率的关键句,确定单位“1”的量,然后根据线段图写出等量关系式,最后根据已知条件和问题列式解答。这里需要注意的是,单位“1”的确定是关键,它通常隐藏在含有分数的关键句中,或者当句子中的单位“1”不明显时,可以把原来的量看作单位“1”。
在分数乘法的应用中,还有一些需要注意的概念。例如,“增加”、“提高”等词汇蕴含“多”的意思,“减少”、“下降”等则蕴含“少”的意思。在解决应用题时,应准确理解这些词汇的含义,以便正确列出算式。
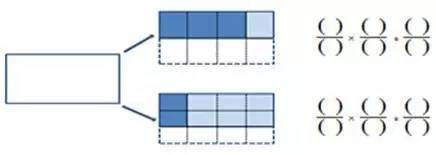
为了加深学生对分数乘法的理解,练习题的设计也至关重要。通过填空、选择、解答等多种形式的练习,学生可以更好地掌握这一知识点。例如,在填空题中,学生通过动手涂一涂、算一算的方式,可以直观地理解分数乘整数的意义;在选择题中,学生需要仔细分析题目中的数据特征,运用所学知识做出正确判断;在解答题中,学生则需要综合运用所学知识解决实际问题。
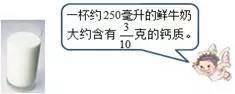


通过这些练习,学生不仅能够巩固所学知识,还能提高解题能力和逻辑思维能力。分数乘法作为数学学习中的一个重要部分,对学生的全面发展具有不可替代的作用。希望每位学生都能在数学的世界里找到属于自己的乐趣和成就。